文章目录
深度学习模型概述
深度学习特征
机器学习VS深度学习
- 机器学习:低功率,简单模型
- 深度学习:高功率,复杂模型
在拥有强大的处理能力之前,训练高功率模型将需要很长的时间;在拥有大量的数据之前,训练高功率模型会导致过度拟合问题。二者一些区别主要体现如下:
- 数据依赖:深度学习需要大量数据,否则容易过度拟合
- 硬件依赖:存在大量矩阵运算,对GPU依赖高
- 执行时间:深度学习参数很多,需要更多时间
- 领域知识依赖:机器学习障碍主要是特征工程步骤,需要领域专家和很多领域知识人工手动识别和标记特征;深度学习尝试从数据中直接获取更高等级的特征,减少对每个问题设计和构造特征的工作
- 问题解决模式:传统会拆分为子问题,再合并;深度学习更加强调端到端问题解决
- 可解释性:传统机器学习一般会给出很清楚的解释说明(决策树,线性/逻辑回归),但深度学习不会清楚告诉你神经网路协同具体是如何工作的,结果是如何一步步产生的
神经网络的学习任务
一般业界会把深度学习和神经网络作为同一个概念进行表达
神经网络学习任务分类和机器学习类似:
- 监督学习:分类问题和回归问题
- 非监督学习
- 强化学习
【图形讲解】
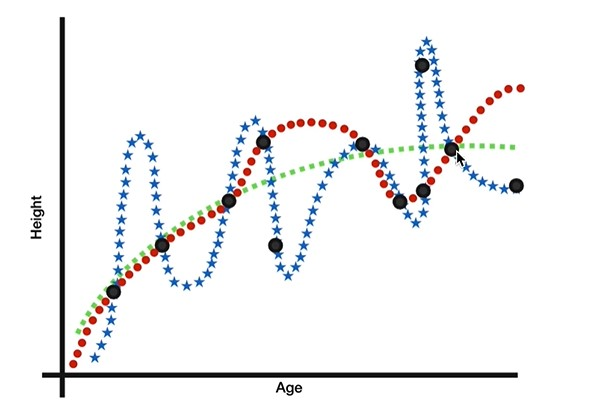
监督学习回归预测:年龄和身高
黑点是样本点,三种颜色表示:预测拟合情况
红色:年龄无限接近1的时候是没有身高的,当年龄增大,会有一定波动,大部分样本点还是在红色线上的
蓝色:百分百拟合,所有样本点都在蓝色线上
绿色:最平滑,大约只有一半样本点在线上,但时不在线上的样本点,差距不大
结论:绿色的更加客观,泛化能力更强
新样本在预测模型的好坏程度,我们称之为:泛化能力
什么是神经网络
- 神经元:承担计算的基本单元
每一个独立的神经元进行一个简单的函数运算
神经元的互相关系和连接促进了大脑的复杂功能
【神经元解构】
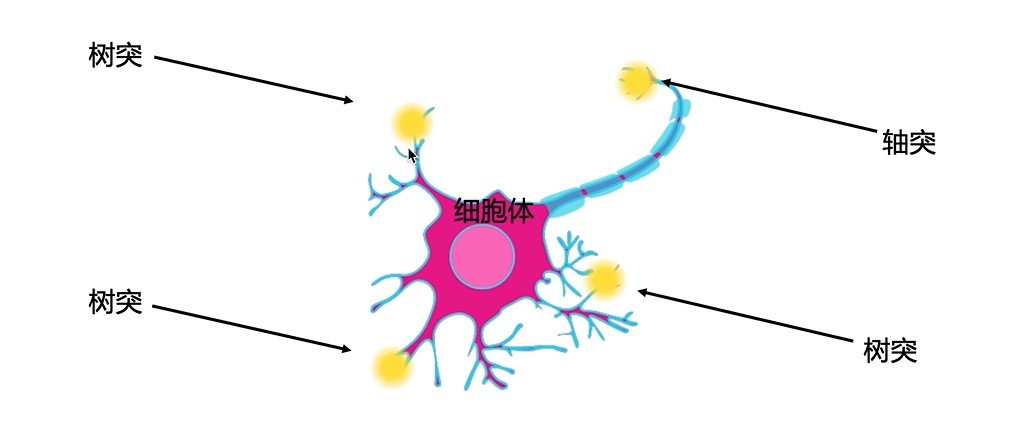
- 树突:接收信号
- 细胞体:运算主题
- 轴突:连接其它神经元树突,传递信息
【实例解构神经网络】
想象你是一名银行职员,现在需要预测每个客户次年的交易额
首先这是一个回归任务
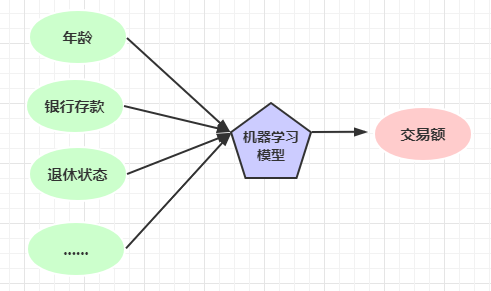
机器学习做法,用一个传统机器学习模型去拟合,学习样本特征
神经网络的做法,神经元之间计算传递信息
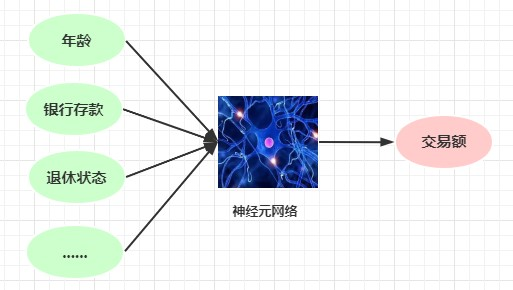

实际上整个神经网络会分多层(也不是越多越好),某个神经元计算结果会传递给下一层中每个神经元
随着层数和神经元个数越多,计算越复杂
搭建神经网络
常见工具包封装了常用的神经网络算法,我们只要调用它们提供的API,通过几行代码就能实现很复杂的神经网络构建

- Tensorflow(google):初期是面向工程师的,随着迭代,易用性逐渐提高
- PyTorch(facebook):与Tensorflow也越来越像,社群和资源二者都差不多
- K:前端API,需要后端支持,比如Tensorflow,无法单独使用
这些工具框架,熟悉一个就行了,搭建神经网络的理论方法:
- 选择使用合适工具包
- 构造方式定义好三层:
> 1 输入层:接收样本特征,一般个数和样本特征数一致
2 隐藏层:除去输入和输出所有中间层,一般由工具构造产生
3 输出层:分类任务的话,输出就等于总的标签数量;回归任务的话,一般只有一个输出
全连接神经网络:某神经元会和下一层所有神经元联接
卷积神经网络:计算和联结方式会有少许的不同
对于使用工具包的我们来说,只是调用不同的函数而已
深度学习框架
PyTorch介绍
为什么使用PyTorch(https://pytorch.org/)
- 易用,所见即所得,动态计算
- 与NumPy很相似,可以直接移植
- 强大便利的GPU支持
- 便捷的自动求导功能,对深度学习训练帮助很大
PyTorch基本操作
- 创建张量(PyTorch中基础运算单位)

2X2的张量,0-1的均匀分布
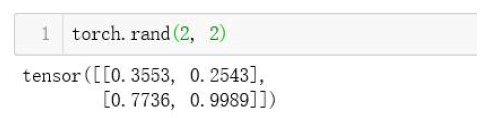
张量拥有形状、数据类型属性
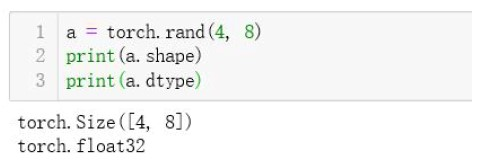
【矩阵乘法知识】

- 矩阵操作:矩阵相乘方法:matmul

PyTorch的自动求导
在一维函数里求导,我们称之为导数;在多维函数里求导,我们称之为梯度
- 自动求梯度
通过randn创建了一个标准正态分布的张量,requires_grad表示是否要求梯度,会自动开启自动求梯度功能

发现用户自己创建的Tensor,grad_fn梯度函数是None,这个函数表示某个变量的梯度是通过这个函数来求解的

梯度传播性,x变量产出y也是有梯度的

z代表的是一个乘法运算梯度函数,mean表示均值计算,这些基本加减乘除梯度算法,在PyTorch里都是固定写好的 -
梯度计算(实际计算)

out.backward相当于对out进行求导,out涉及中间变量都会参与梯度计算,所以我们可以打印出x的梯度计算结果
这个过程称之为链式求导
- 链式求导(梯度计算底层原理)

out对x求导就是y,也就是x+2,最后结构符合预期
基于PyTorch的网络构建
自己构建三层做法示例:

使用PyTorch做法示例:利用new network(nn)
定义神经网络阶段

实际使用阶段
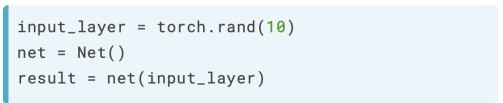
input_layer会直接作为参数调用forward函数
搭建神经网络
卷积层
- 卷积 convolution
计算机视觉领域,数据输入格式:B(图片数量) x C(通道数) x W(宽度) x H(高度),称作BCWH格式

原始的5x5图片,提取特征值过程

这个filter称作卷积核,维度可以自己去设置
filter就是一个算子,传统机器学习中算子一般是人为设定的,在卷积神经网络里,算子一般是可变的,是学习出来的
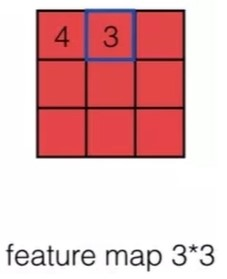
卷积计算过程,就是使用算子覆盖原始图片,进行矩阵乘法计算出结果的过程
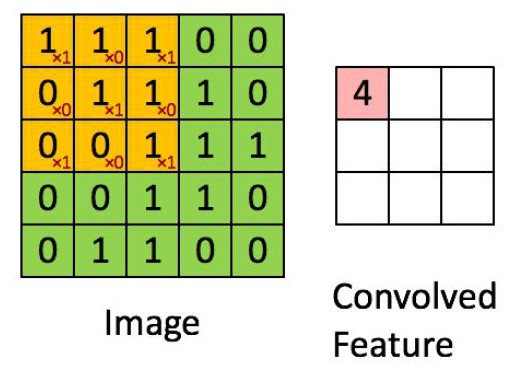
上面这个维度的滑动被称作WH维度,除此之外我们还要进行C(通道)维度的卷积计算
C维度卷积计算,此处C我们选取的是RGB颜色,值为3

W0是三个卷积核,对3个通道进行卷积核计算,得到一组值
W1也是三个卷积核,对3个通道进行卷积核计算,得到一组值
灰色叫做pading,补白扩大尺度,保证输入和输出是相同的
O:output,表示输出尺寸大小
I:input:表示输入尺寸大小
P:pading,补白尺度
K:卷积核
S:步长,滑动时移动的格数
转置卷积

输入是4x4的,卷积核是3x3的,计算之后得到一个2x2的正常卷积
将结果改成矩阵形式,将4x4的拉伸成16x1的矩阵

将3x3的卷积核变成4x16的稀疏矩阵
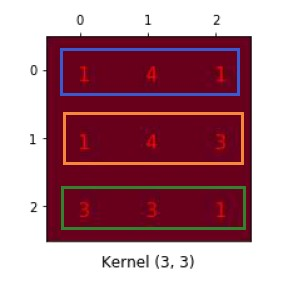
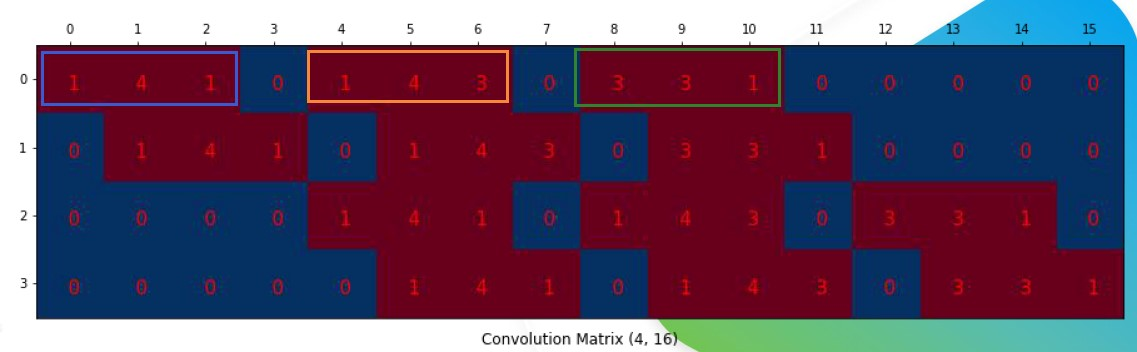
将稀疏矩阵和拉伸后的矩阵相乘计算,得到4x1的矩阵
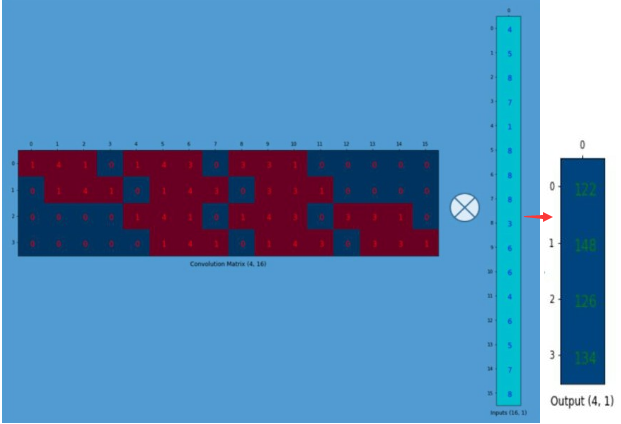
对稀疏矩阵和原始输入拉伸矩阵进行转置,然后进行相乘(卷积计算),得到16x1矩阵
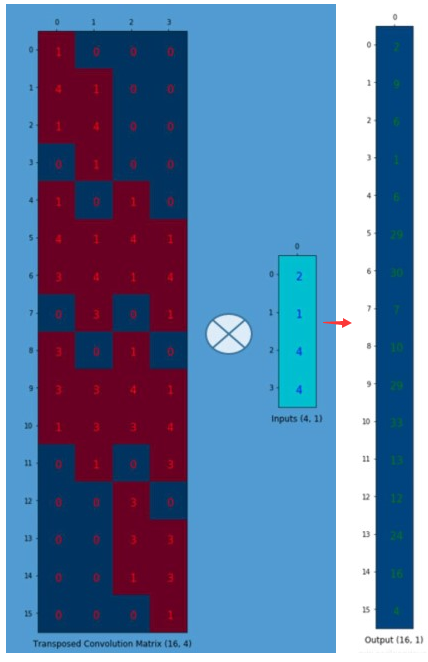
转置卷积,有的地方又叫反卷积,但是其实并不完全准确,数值上请其实并无法恢复
池化层
池化层和卷积层很类似,但是它的操作更加简单,它没有任何参数需要去学习
- 平均池化:对kernel窗口里区域求平均值,只对当前通道做操作

-
最大池化:对kernel窗口里区域取最大值,这个特性神经网络中还是比较有用的

-
全局池化 :kernel大小对与整个数据块的大小
全局平均池化 GAP
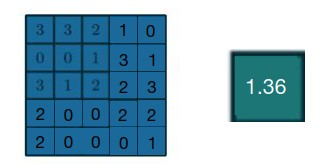
全局最大池化GMP

池化层作用和特点
- 无参数,运算速度快
- 下采样(不做参数运算),降低特征图大小,减小计算量
- 最大池化具有一定的非线性
- 变相扩大感受野
- 不变性(平移、旋转、尺度),不能绝对保证
激活函数
sigmoid
是神经网络中很重要的一层,常用有:
- SIgmoid:优雅曲线,存在梯度消失问题
- ReLU:存在死亡区域和非零均值问题
- Leaky ReLU /PReLU:非饱和
- ELU:整体最优雅,但有额外的计算量

sigmoid激活函数,表示一种概率,一般会放在最后一层,它的特点: -
非线性(拟合函数本身复杂,肯定不是线性能够表示的)
- 双侧饱和(正负无穷有趋向的固定值)
- 梯度消失(曲线斜率趋向于0,有一定风险)
ReLU
修正线性单元(ReLU):大于0去本身,小于0变为0
- 非线性
- 单测饱和:具有开关特性;特征选择(去掉不要特征参数);抑制噪声(噪声是高频信息)
- 梯度0、1
- 非零均值(数据分布是偏向正半轴的,但神经网络一般都是希望平均分布的)
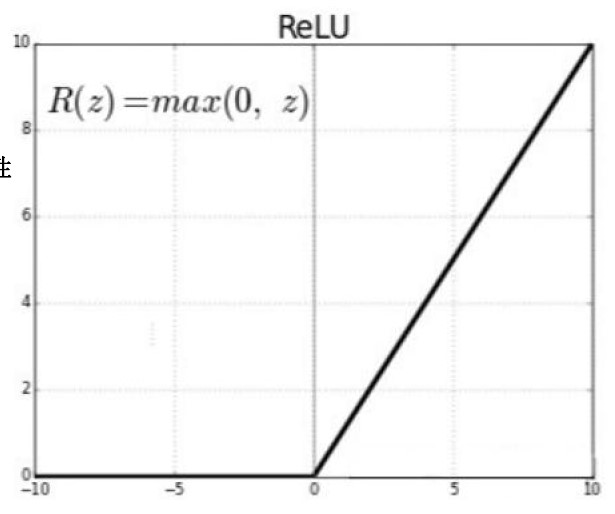
开关的作用未必能起到实际作用,是需要不断学习的,如果一开始参数设置错误,可能参数就失效了
PReLU
Leak ReLU/Patametrized ReLU(PReLU):改进ReLU死亡区域问题
- 非线性
- 无饱和性,无法做到完全关闭某些特征
- 梯度:a和1,参数需要做实验(参数学习)去做选择
- 接近零均值
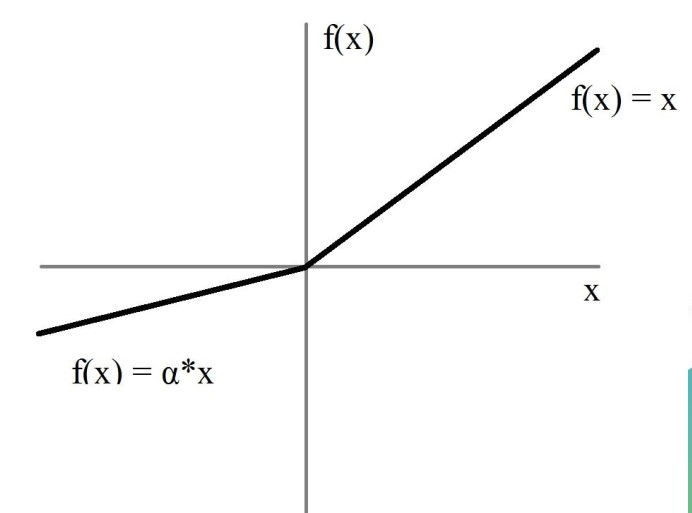
ELU
ELU:优化了饱和性
- 非线性
- 单侧饱和
- 梯度ae^x,1,有了梯度一些参数特征学习过程中还有机会调整回来
- 接近零均值
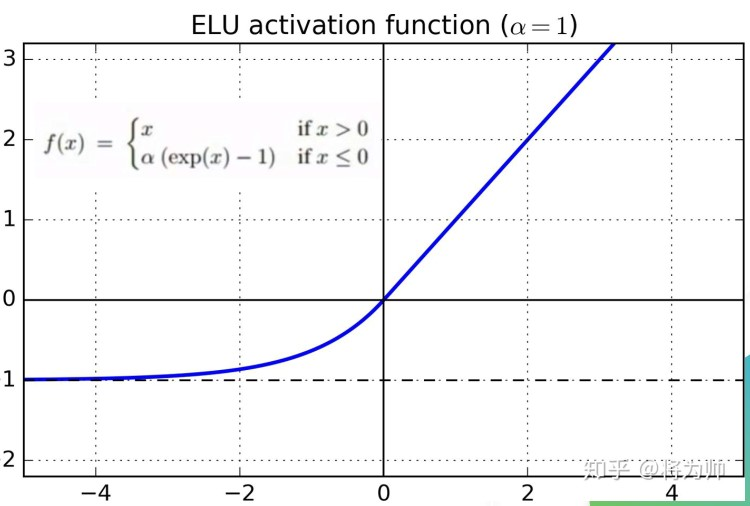
特点看起来很好,但是计算量是最大的,还是要根据具体实验来定,毕竟神经网络是经验型科学,常用的还是ReLU模型
激活函数的作用和特点:
- 为网络提供非线性拟合能力
- 具有特征选择和抑制噪声的能力
- 相比sigmoid有效缓解了梯度消失的问题
其他功能层
归一化层(BN)
主要功能如下:
1 每一个通道求均值(BHW)
2 求方差
3 归一化
4 尺度和平移

可以合成一个表达公式:

练时采用当前均值方差,并更新移动平均的均值和方差
预测时采用移动平均的均值和方差
归化层的作用和特点:
- 加快网络训练的收敛速度
- 防止梯度消失和梯度爆炸
- 降低过度拟合程度
Dropout层
为了正则化而诞生的,从稠密变成稀疏,具有随机性
- 训练时以概率p抑制某些节点
- 预测时所有节点乘p
- 降低过度拟合程度
- 防止单点依赖

正则化,也可以降低过度拟合程度,一般有两种:
- L1正则化


-
L2正则化
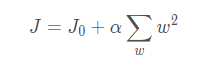

一般我们会取离优化中心(彩色圈层部分)最近的切点作为结果值
 菡萏如佳人
菡萏如佳人